コンテンツ

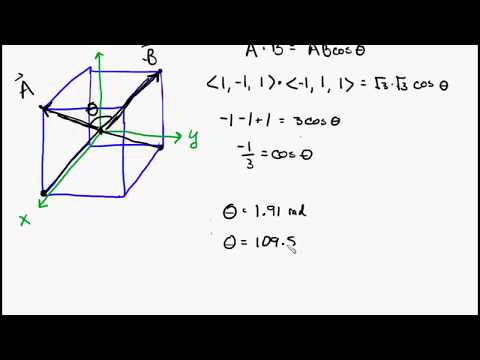
正方形を作成して2本の対角線を描く必要がある場合、それらはその中心で交差し、4つの直角三角形を形成します。 2本の線は90度の角度で交差します。立方体のこれらの2つの対角線が、それぞれ1つのコーナーから他のコーナーに走り、中央で交差していることも直角に交差できることを直感的に発見できます。しかしそれは間違いでしょう。 2つの対角線が交差する角度の決定は、最初に見るよりも少し複雑ですが、ジオメトリと三角法の原理を理解することをお勧めします。
ステップ1
エッジの長さを単位として定義します。定義により、立方体の各エッジの長さは湿気と同じです。
ステップ2
ピタゴラスの定理を使用して、1つのコーナーから同じ側の別のコーナーに向かう対角線の長さを決定します。これは、明確にするために「マイナー対角線」と呼ぶことができます。形成された直角三角形の各辺は単位であるため、対角線は√2に等しくなければなりません。
ステップ3
ピタゴラスの定理を使用して、立方体の反対側にある1つのコーナーから別のコーナーまでの対角線の長さを決定します。これは、「主対角線」と呼ぶことができます。 1辺が1単位に相当する直角三角形と、2単位の平方根に相当する「小さい対角線」に相当する辺が1つあります。斜辺の2乗は辺の2乗の合計に等しいため、斜辺は√3でなければなりません。キューブの反対側の1つのコーナーから他のコーナーに伸びる各対角線は、√3単位に等しくなります。
ステップ4
立方体の中心を横切る2つの大きな対角線を表す長方形を描画し、それらの交点の角度を見つける必要があることを考慮してください。この長方形は、高さが1単位、幅が√2単位でなければなりません。大きな対角線がこの長方形の中心で交差し、2つの異なるタイプの三角形を形成します。それらの1つは1ユニットに等しい辺と他の2つは√3/ 2(大きい対角線の長さの半分)に等しくなります。もう1つの辺は√3/ 2に等しい2つの辺を持ちますが、最初の辺は√2になります。三角形の1つを分析し、最初の三角形を選択して、未知の角度を発見するだけです。
手順5
三角関数式「c²=a²+b²-2ab x cos C」を使用して、この三角形の未知の角度を見つけます。 「C = 1」、「b」と「a」は√3/ 2に等しい。これらの値を方程式に入れると、角度の余弦が1/3であることがわかります。コサイン1/3の逆は70.5度の角度に対応します。