
コンテンツ
カテナリーとは、ケーブルが両端で支えられているときにケーブルがとる形状で、ケーブルの重さの作用のみを受けます。特に吊り橋の建設に広く使用されており、逆のカテナリーは古代からアーチの建設に使用されてきました。懸垂曲線は、放物線に似た「U」字型の双曲線余弦関数です。特定のカテナリーの形状は、そのスケール係数によって決定できます。
カテナリーの計算
ステップ1
標準カテナリー関数y = a cosh(x / a)を計算します。yはデカルト平面のy、xはデカルト平面のx、coshは双曲線余弦関数、 "a"はスケールファクターです。
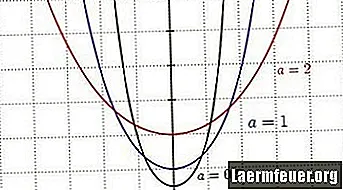
ステップ2
カテナリーの形状に対するスケール係数の影響を観察します。単位長さあたりのケーブルの重量に対するケーブルの水平張力の比と考えることができます。スケール係数が小さいほど、カーブは深くなります。
ステップ3
別の方程式でカテナリー関数を計算します。方程式「y = a cosh(x / a)」は、「y = a / 2(e ^(x / a)+ e ^(-x / a))」と数学的に同等であると証明できます。 「自然対数の基礎であり、約2.71828です。
ステップ4
「y = yo /(1 + et)」などの弾性カテナリーの関数を計算します。「yo」は単位長さあたりの開始質量、「e」はばね定数、「t」は時間です。この方程式は、吊り下げケーブルの代わりに跳ねるばねを表しています。
手順5
カテナリーの実際の例を計算します。関数「y = -127.7 cosh(x / 127.7)+ 757.7」は、「セントルイスアーチ」(セントルイスのアーチ)を表し、測定値はフィート単位です。