
コンテンツ
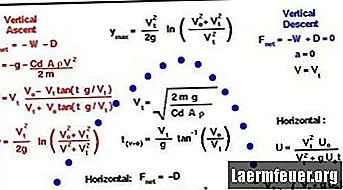
弾丸の弾道、具体的には空中での時間、弾道の範囲と最高点を計算する方法は次のとおりです。この例では、計算を簡略化するためにいくつかの仮定が行われました。無視できる空気抵抗、風がなく、地球の回転が有効になるための発射距離が不十分です。
空中での時間を決定します。
ステップ1
最初に、弓の形状を決定する必要があります。角度が最初は下向きである場合、最も高い点は発砲位置であることが既にわかっています。上向きの角度でも、この角度が浅いか、十分な高さ(h)であるかに関係なく、ターゲットを最高点にすることができます。これは、放送時間が決定されたときに、ステップ4で決定できます。
ステップ2
角度「?」なら発射率は、発射体の初期軌道と水平線の間の速度であるため、初期垂直速度はV(i)= V.sen?です。
ステップ3
放送時間は、位置の式h = V.sen?.T-(0.5)g.t ^ 2を使用して求められます。ここで、g = 9.8メートル/秒^ 2です。空中での時間tを除くすべての変数が既知であるため、これは2次関数を使用して解決できます:ax ^ 2 + bx + c = 0したがって、x = [-b±√(b ^ 2-4ac )] / 2a
ステップ4
tの複数の解が許可されている場合、h> 0なので、最初の結果は上昇経路で高さ= hの場合に対応し、2番目の結果は下降経路で高さ= hの場合に対応します。 h <0の場合、tの唯一の実数解が許可され、もう1つは負です。
最大の高さを決定する
ステップ1
<?の場合、最大の高さが初期の高さh = 0であることが既にわかっています。
ステップ2
弾丸がhを延長する時間tが複数あった場合、最小のtはhが最高点である飛行経路に対応します。最高のtは、弾丸がhに戻る前により高い高さに到達することに対応します。この高さを解決するには、式V(t)= V(0)-9.8tを使用して、垂直速度がゼロ。つまり、t、V.sen?= 9.8t。?
ステップ3
tを解決して高さの式を接続すると、最大の高さが得られます。hm= V.sen? -4.9トン^ 2。 tの解が1つだけ許可された場合、同じアプローチが最大高さの解に使用されます。
移動した水平距離を決定します。
ステップ1
弾丸が高さhに到達するまでの水平距離を決定するには、最初に弾丸の初期水平速度を計算します。v(i)= V.cos(?)。
ステップ2
水平速度を使用する式の位置で、弾丸が最終的な高さAに到達する時間tを代入します。A=V.cosΘ.t。右側に空気抵抗がなく、加速項がないと仮定します。
ステップ3
高さがhのときに複数の時間tがあった場合、「A」の2つの位置が有効になり、到達した最高点は2つの「A」のうち小さい方のhmになります。水平および垂直の終了位置と到達した最高点がわかったので、弾丸の軌道が決まります。